Bất đẳng thức logarit là gì và những điều cần biết

Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường.  Một trong số đó là bất đẳng thức logarit. Vậy bất đẳng thức logarit là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!

Logarit là gì?

Cho hai số dương a và b với a≠1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.

Phương pháp biến đổi và cách giải bất đẳng thức logarit

Có nhiều phương pháp biến đổi để chúng ta có thể ứng biến trong nhiều trường hợp khác nhau mà Reviewedu.net sẽ mang lại cho các bạn dưới đây. Hãy cùng chúng mình tham khảo nhé!

Phương pháp biến đổi

• Bất phương trình mũ cơ bản

Bất phương trình   hoặc

Bất phương trình 

Bất phương trình

Phương pháp giải

 Đưa về cùng cơ số

Phương pháp mũ hóa

Bài tập ứng dụng bất đẳng thức logarit

Bài tập 1. Cho bất phương trình log7 (x2 + 2x + 2) + 1 > log7 (x2 + 6x + 5 + m). Có bao nhiêu giá trị nguyên của tham số m để bất phương trình trên có tập ngiệm chứa khoảng (1; 3)?

A. 35             B. 36               C. 34          D. 33

Giải:

BPT

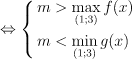, với f(x) = –x2 – 6x – 5; g(x) = 6x2 + 8x + 9

Xét sự biến thiên của hai hàm số f(x) và g(x)

f’(x) = –2x – 6 < 0, ∀ x ∈ (1; 3) ⇒ f(x) luôn nghịch biến trên khoảng (1; 3)

g’(x) = 12x + 8 > 0, ∀ x ∈ (1; 3) ⇒ g(x) luôn đồng biến trên khoảng (1; 3)

Khi đó –12 < m < 23

Mà m ∈ ℤ nên m ∈ {–11; –10; …; 22}

Vậy có tất cả 34 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Bài tập 2. Gọi S là tập tất cả các giá trị nguyên của tham số m để bất phương trình log2 (7x2 + 7) ≥ log2 (mx2 + 4x + m) có tập nghiệm là ℝ. Tổng các phần tử của S là

A. 10                B. 11              C. 12             D. 13

Giải:

BPT có tập nghiệm ℝ , ∀ x ∈ ℝ

Ta có:

Ta có:

Do đó 

Mà m ∈ ℤ nên m ∈ {3; 4; 5}

Vậy S = 3 + 4 + 5 = 12.

Xem thêm:

Bất đẳng thức lượng giác

Bất đẳng thức cosi

Bất đẳng thức cơ bản