Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức cơ bản mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Vậy những bất đẳng thức cơ bản đó gồm những gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức là gì?
- Trong toán học, một phát biểu về quan hệ thứ tự giữa hai đối tượng, với hai đối tượng là các biểu thức chứa các số và các phép toán được gọi là bất đẳng thức.
- Biểu thức phía bên trái dấu bất đẳng thức được gọi là vế trái. Biểu thức phía bên phải được gọi là vế phải của bất đẳng thức.
Một số bất đẳng thức cơ bản đáng nhớ
Dưới đây là một số những bất đẳng thức cơ bản mà đa số các bạn học sinh đều đã gặp qua trong suốt 12 năm học của bản thân. Hãy cùng điểm qua nhé!
Bất đẳng thức mincopxki
Bất đẳng thức Minkowski (Minkowski)
Với mọi số thực a,b,x,y ta có
Đẳng thức xảy ra khi và chỉ khi ay=bx (hay còn viết dưới dạng tỉ lệ a/x=b/y, với quy ước nếu mẫu số bằng 0 thì tử số cũng bằng 0).
Bất đẳng thức Minkowski tổng quát
Với p>1 và mọi số thực xi ,yi
hay
Dấu bằng xảy ra khi và chỉ khi
x1/y1=x2/y2=…=xn/yn.
Bất đẳng thức cosi
Bất đẳng thức Cosi có thể được phát biểu một cách khái quát như sau:
Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng. Trường hợp trung bình cộng và trung bình nhân của chúng chỉ bằng nhau khi n bằng nhau.
Phát biểu này có thể được trình bày như sau:
Với 2 số thực a và b (a, b > 0, R), ta có:
a + b2ab
Dấu “=” xảy ra a=b
Bất đẳng thức này cũng áp dụng với n số thực dương:
x1 + x2 + … + xn x1.x2…..xn (n>1, N)
Dấu “=” xảy ra x1=x2=…=xn
Bất đẳng thức chebyshev
Trong toán học, Bất đẳng thức cộng Chebyshev, được đặt theo tên nhà toán học Pafnuty Chebyshev, được phát biểu rằng: Nếu cho
và
thì
Tương tự, nếu
và
thì
Bất đẳng thức cauchy-schwarz
Trong toán học, bất đẳng thức Cauchy–Schwarz , còn được gọi là bất đẳng thức Schwarz , bất đẳng thức Cauchy , hoặc bằng cái tên khá dài là bất đẳng thức Cauchy–Bunyakovski–Schwarz. Là một bất đẳng thức thường được áp dụng trong nhiều lĩnh vực khác nhau của toán học, chẳng hạn trong đại số tuyến tính dùng cho các vector, trong giải tích dùng cho các chuỗi vô hạn và tích phân của các tích, trong lý thuyết xác suất dùng cho các phương sai và hiệp phương sai.
Bất đẳng thức này phát biểu rằng nếu x và y là các phần tử của không gian tích trong thực hay phức thì
Dấu đẳng thức xảy khi và chỉ khi x và y phụ thuộc tuyến tính (hay nói theo ý nghĩa hình học là chúng song song với nhau). Một trường hợp đặc biệt nữa của x và y là khi chúng trực giao (hay nói theo ý nghĩa hình học là vuông góc) nhau thì tích trong của chúng bằng zero.
Như vậy, có vẻ như bất đẳng thức này cho thấy có mối liên quan giữa khái niệm “góc của hai vectơ” với khái niệm tích trong, mặc dù các khái niệm của hình học Euclide có thể không còn mang đầy đủ ý nghĩa trong trường hợp này, và ở mức độ nào đấy, nó cho thấy ý niệm các không gian tích trong là một sự tổng quát hoá của không gian Euclide.
Bất đẳng thức bunhiacopxki
- Bất đẳng thức Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, do ba nhà toán học độc lập phát hiện và đề xuất, có nhiều ứng dụng trong các lĩnh vực toán học. Thường được gọi theo tên nhà Toán học người Nga Bunhiacopxki.
- Bất đẳng thức này rất quen thuộc và thường được ứng dụng rất nhiều trong các bài toán về bất đẳng thức và cực trị.
Bất đẳng thức Bunhiacopxki dạng cơ bản:
Bất đẳng thức Bunhiacopxki cho 2 bộ số:
Với quy ước nếu một số nào đó (i = 1, 2, 3, …, n) bằng 0 thì tương ứng bằng 0
Bất đẳng thức bernoulli
Trong toán học, bất đẳng thức Bernoulli là một bất đẳng thức cho phép tính gần đúng các lũy thừa của 1 + x.
Bất đẳng thức này được phát biểu như sau:
<math>(1 + x)^r \geq 1 + rx\!</math>
với mọi số nguyên r ≥ 0 và với mọi số thực x > −1. Nếu số mũ r là chẵn, thì bất đẳng thức này đúng với mọi số thực x. Bất đẳng thức này trở thành bất đẳng thức nghiêm ngặt như sau:
<math>(1 + x)^r > 1 + rx\!</math>
với mọi số nguyên r ≥ 2 và với mọi số thực x ≥ −1 với x ≠ 0.
Bất đẳng thức Bernoulli thường được dùng trong việc chứng minh các bất đẳng thức khác.
Bất đẳng thức am-gm
- Khi một bất đẳng thức đúng với mọi giá trị của tất cả các biến có mặt trong bất đẳng thức, thì được gọi là bất đẳng thức tuyệt đối hay không điều kiện.
- Khi một bất đẳng thức đúng với một số giá trị nào đó của biến, với các giá trị khác thì nó bị đổi chiều hay không còn đúng nữa thì được gọi là một bất đẳng thức có điều kiện. Một bất đẳng thức đúng, sẽ vẫn đúng nếu cả hai vế của nó được thêm vào hoặc bớt đi cùng một giá trị, hay nếu cả hai vế của nó được nhân hay chia với cùng một số dương.
- Một bất đẳng thức sẽ bị đảo chiều nếu cả hai vế của nó thực hiện nhân hay chia bởi một số âm. Đây là những kiến thức cơ bản nhưng quan trọng cho các bất đẳng thức đáng nhớ.



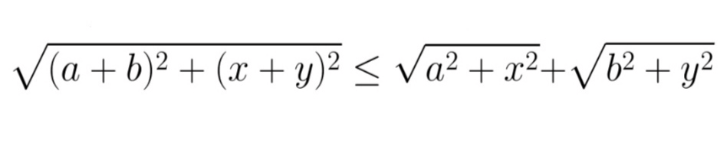
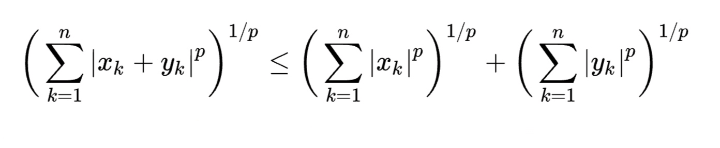
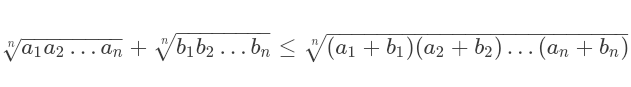
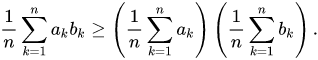
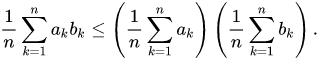


bất đẳng thức cosi là gì ạ?
có những bất đẳng thức nào?
Bất đẳng thức am-gm là gì?