Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức bunhiacopxki. Vậy bất đẳng thức bunhiacopxki là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức bunhiacopxki là gì?
- BĐT Bunhiacopxki có tên gọi chính xác là bất đẳng thức Cauchy – Bunhiacopxki – Schwarz, do ba nhà toán học độc lập phát hiện và đề xuất, có nhiều ứng dụng trong các lĩnh vực toán học. Thường được gọi theo tên nhà Toán học người Nga Bunhiacopxki.
- Bất đẳng thức này rất quen thuộc và thường được ứng dụng rất nhiều trong các bài toán về bất đẳng thức và cực trị.
Bất đẳng thức dạng cơ bản:
Bất đẳng thức cho 2 bộ số:
Với quy ước nếu một số nào đó (i = 1, 2, 3, …, n) bằng 0 thì tương ứng bằng 0
Bài tập ứng dụng bất đẳng thức bunhiacopxki
Bài 1: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
Lời giải:
Áp dụng bất đẳng thức ta có:
(điều phải chứng minh)
Dấu “=” xảy ra khi và chỉ khi a = b = c
Bài 2: Tìm giá trị lớn nhất của biểu thức ![]()
Lời giải:
Áp dụng bất đẳng thức ta có:
Vậy max A = 2 khi và chỉ khi x = 3
Các hệ quả của bất đẳng thức
Sau đây là các hệ quả của bất đẳng thức:
- Hệ quả 1:
- Hệ quả 2:
Xem thêm:



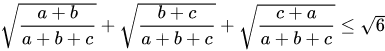
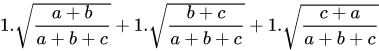
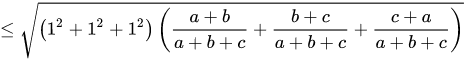
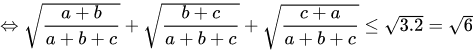
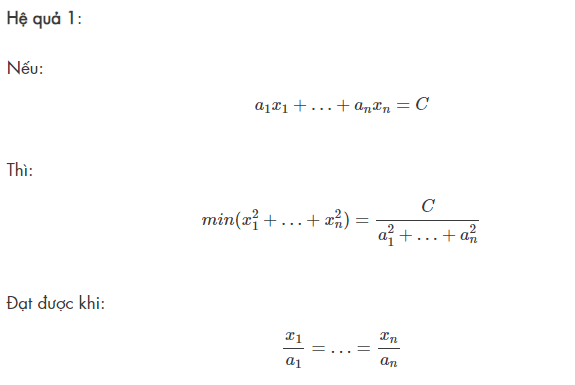
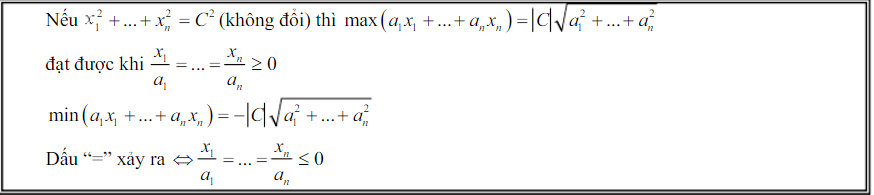


đây là bất đẳng thức gì vậy ạ?
có mấy hệ quả?
bất đẳng thức này khó không?