Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho tất cả các bạn học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức lượng giác. Vậy bất đẳng thức lượng giác là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức lượng giác là gì?
1. BĐT lượng giác xoay quanh sin, cos, tan, cot rất cần thiết trong quá trình học toán và giải bài tập của các bạn học sinh.
Chứng minh bất đẳng thức lượng giác
BĐT lượng giác bao gồm hai nhánh:
- BĐT lượng giác không có điều kiện.
- BĐT lượng giác có điều kiện.
BĐT lượng giác không có điều kiện
Ví dụ: Chứng minh rằng với mọi α, ta luôn có bất đẳng thức :
4sin3α+5≥4cos2α+5sinα
Lời giải:
Bất đẳng thức (BĐT) đã cho tương đương với BĐT sau :
4(3sinα−4sin3α)+5≥4(1−2sin2α)+5sinα
4(3sinα−4sin3α)+5≥4(1−2sin2α)+5sinα
⇔16sin3α−8sin2α−7sinα−1≤0
⇔16sin3α−8sin2α−7sinα−1≤0
⇔(sinα−1)(4sinα+1)2≤0(1)
⇔(sinα−1)(4sinα+1)2≤0(1)
Do sinα≤1∀α⇒(1)sinα≤1∀α⇒(1) đúng. Từ đây ta có ĐPCM.
BĐT lượng giác có điều kiện
Chứng minh BĐT :
Bài tập áp dụng BĐT lượng giác
Bài tập 1: Tính các giá trị lượng giác của góc α biết:
Hướng dẫn:
+ Nếu biết trước sinα thì dùng công thức: sin2α + cos2α = 1 để tìm ,
lưu ý:xác định dấu của các giá trị lượng giác để nhận, loại.
+ Nếu biết trước cosα thì tương tự như trên.
+ Nếu biết trước tanα thì dùng công thức: ![]() để tìm cosα
để tìm cosα
lưu ý: xác định tính âm dương của các giá trị lượng giác để nhận, loại. sinα = tanα.cosα, ![]()
Giải
Bài tập 2: Chứng minh đẳng thức lượng giác: (dùng các hằng đẳng thức đại số và các hằng đẳng thức lượng giác cơ bản để biến đổi một vế thành vế kia)
Hướng dẫn:
Xem thêm:




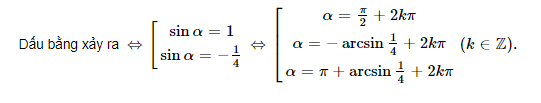
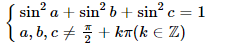


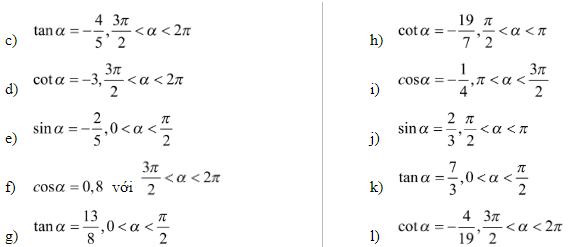
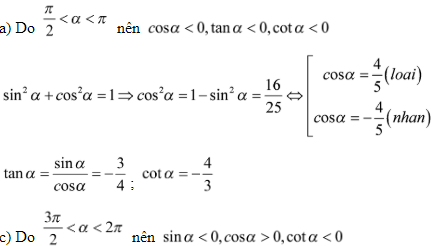
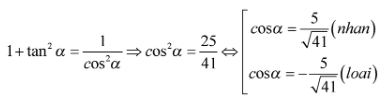
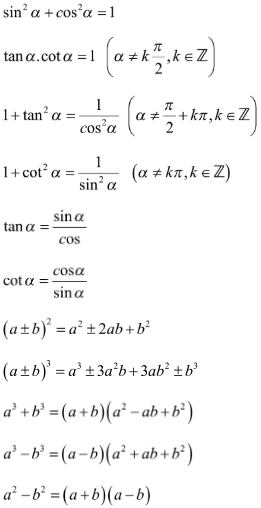
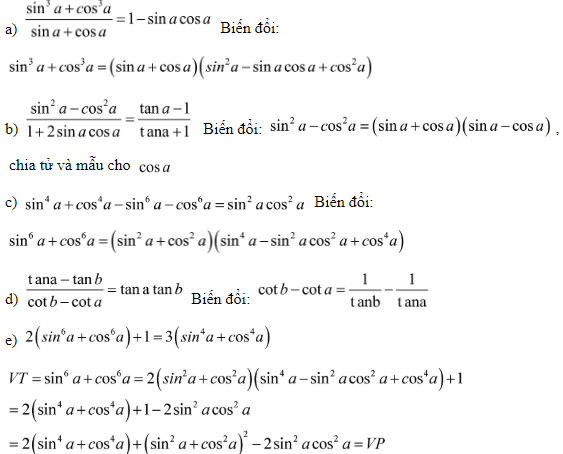


bất đẳng thức này khó không?
Nắm bản chất của bài là được bạn nha!
Lớp 11 học bất đẳng thức này chưa ạ
CHương trình học gần đây đã được thay đổi bạn nha
có chứng minh bất đẳng thức này được không?