Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức hoán vị. Vậy bất đẳng thức hoán vị là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức hoán vị là gì?
Theo toán học, BĐT hoán vị được định nghĩa như sau:
Cho dãy số thực Xn và Yn (n∈N) thỏa mãn:
X1 >= X2 >= … >= Xn
và
Y1 >= Y2 >= … >= Yn
Với mỗi hoán vị ( Z1, Z2,… , Zn) của (X1, X2,… , Xn), ta có:
X1Y1 + X2Y2 + … + XnYn >= Z1Y1 + Z2Y2 + … + ZnYn >= XnY1 + Xn -1Y2 + …+ X1Yn
Đẳng thức xảy ra khi một trong 2 dãy là “dừng”, hoặc ( Z1, Z2,… , Zn) đồng bậc với (X1, X2,… , Xn) hoặc ( Xn,…, X2, X1)
Các hệ quả của bất đẳng thức hoán vị
Hệ quả: Cho dãy số thực (Xn), (n∈N) và ( Z1, Z2,… , Zn) là một hoán vị của (X1, X2,… , Xn), ta có:
- (X1)^2 + (X2)^2 +…+ (Xn)^2 >= X1Z1 + X2Z2 + … + XnZn
- (Z1/X1) + (Z2/X2) + (Zn/X2) >= n
Chứng minh BĐT hoán vị
Bất đẳng thức đã cho tương đương với:
Y1(X1 – Z1) + Y2(X2 – Z2) + Y3(X3 – Z3) + … + Y(Xn – Zn)>= 0
Theo khai triển Abel ta có:
Y1(X1 – Z1) + Y2(X2 – Z2) + Y3(X3 – Z3) + … + Yn(Xn – Zn)
= (Y1 – Y2)(X1 – X2) + (Y2 – Y3)(X1 + X2 -Z1 -Z2) + (Y3 – Y4)X1 + X2 + X3 -Z1 – Z2 – Z3)
+…+ (Yn-1 – Yn)( X1 + X2 +… + Xn-1 – Z1 – Z2 – Zn-1) + Yn( X1 + X2 +… + Xn – Z1 – Z2 – Zn)
Do X1>= X2>= … >= Xn và Y1>= Y2>= … >= Yn nên tổng trên luôn lớn hơn hoặc bằng 0. Bất đẳng thức đã cho được chứng minh.
Bài tập ứng dụng BĐT hoán vị
Bài tập 1: Cho các số không âm x, y ,z thõa mãn x + y + z =1. Chứng minh rằng:
Xem thêm:



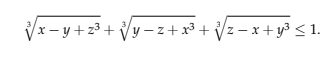





chứng minh bất đẳng thức này như thế nào?
bất đẳng thức có những hệ quả nào?
có bài tập ví dụ không ạ?