Lý thuyết về hình bình hành cũng như cách chứng minh một tứ giác là hình bình hành đã được giới thiệu ở chương trình Toán 8, phân môn Hình học. Nhằm giúp các bạn hệ thống lại tất cả các kiến thức cần ghi nhớ từ khái niệm, tính chất, dấu hiệu nhận biết đến cách chứng minh hình bình hành cũng như các bài tập vận dụng, Review Edu đã tổng hợp tất cả ở bài viết dưới đây. Mời các bạn đón đọc!
Hình bình hành là gì?
Hình bình hành là một dạng đặc biệt của hình thang, cụ thể là hình thang có hai cạnh bên song song. Trong hình học Euclide, hình bình hành là hình tứ giác được tạo thành bởi hai cặp đường thẳng song song cắt nhau. Nói đơn giản, hình bình hành là tứ giác có 2 cặp cạnh đối song song.
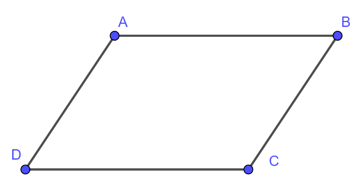
Từ đó ta có, nếu tứ giác ABCD là hình bình hành thì AB//CD và AD//BC
Tính chất của hình bình hành
Hình bình hành là tứ giác có
- Hai cặp cạnh đối song song hoặc một cặp cạnh đối song song và bằng nhau.
- Cặp đường chéo cắt nhau tại trung điểm mỗi đường.
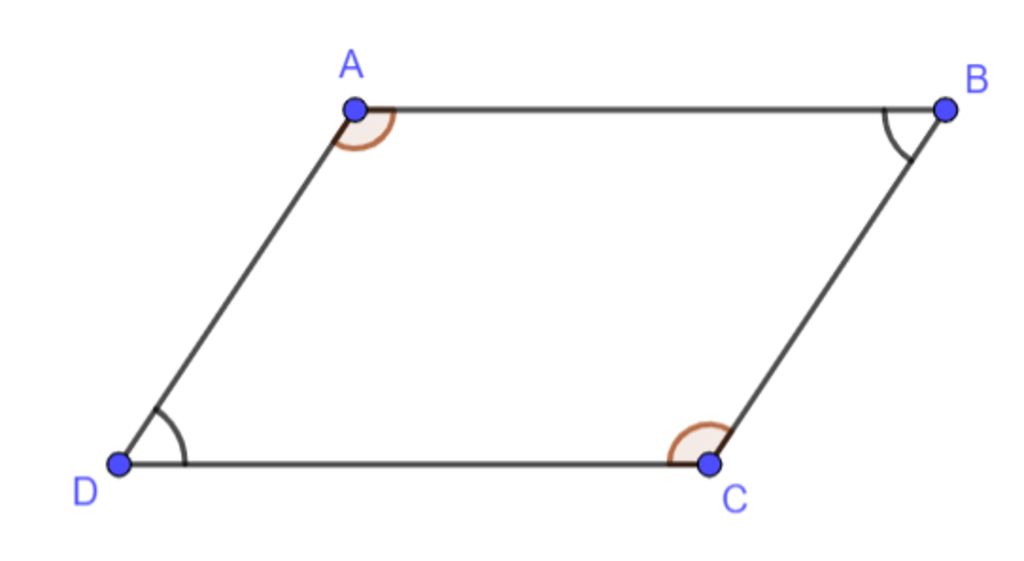
- Hai góc đối bằng nhau.
Dấu hiệu nhận biết hình bình hành
Hình bình hành có 4 dấu hiệu nhận biết sau
- Là tứ giác có hai cặp góc đối nhau bằng nhau
- Là tứ giác có cặp đường chéo cắt nhau tại trung điểm mỗi đường
- Là tứ giác có các cặp cạnh đối song song
- Là tứ giác có 1 cặp cạnh đối vừa // và vừa bằng nhau
- Hình bình hành là hình thang
- Có hai cạnh bên song song
- Có hai cạnh đáy bằng nhau
Cách chứng minh là hình bình hành
Để chứng minh một hình tứ giác là hình bình hành, ta có thể áp dụng tính chất hình bình hành là một tứ giác có 2 cặp cạnh đối diện song song hoặc bằng nhau.
Cách 1: Tứ giác có 2 cặp cạnh đối song song là hình bình hành
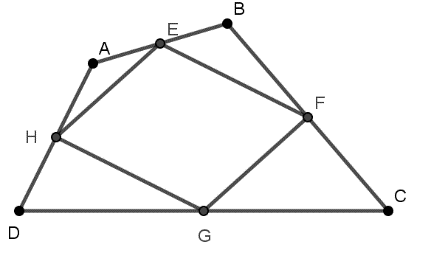
Ví dụ: Cho tứ giác ABCD như hình dưới đây, trong đó
- E là trung điểm của AB
- F là trung điểm của BC
- H là trung điểm của AD
- G là trung điểm của DC
Cho biết tứ giác EFGH là hình gì? Hãy chứng minh điều đó?
Từ hình trên, ta có:
- EF là đường trung bình của △ ABC, suy ra EF // AC (1)
- HG là đường trung bình của △ ADC, suy ra HG // AC (2)
Từ (1) và (2) suy ra được EF // HC
Tiếp theo, ta có:
- FG là đường trung bình của △BDC => FG // BD (3)
- EH là đường trung bình của △BDA => EH // BD (4)
Từ (3) và (4) suy ra FG // EH.
Xét tứ giác EFGH có EF // HG và FG // EH.
=> Tứ giác EFGH là hình bình hành vì có hai cặp cạnh đối song song (ĐPCM)
Cách 2: Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
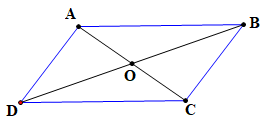
Ví dụ: Cho một tứ giác ABCD như hình, trong đó △ABC = △ADC, chứng minh tứ giác ABCD là hình bình hành?
Dựa theo đề bài, ta có: △ABC = △ADC => AD = BC và AB = DC
=> Tứ giác ABCD là hình bình hành vì có hai cặp cạnh đối bằng nhau.
Bài tập dấu hiệu nhận biết hình bình hành
Các phát biểu sau đây đúng hay sai?
- Tứ giác có 1 cặp cạnh đối nhau bằng nhau là hình bình hành
- Hình thang có hai đáy bằng nhau là hình bình hành
- Hình thang có các cạnh // là hình bình hành
Lời giải:
- Sai vì hình thang cân có một cặp cạnh đối nhau bằng nhau nhưng không phải là hình bình hành
- Đúng vì theo dấu hiệu nhận biết 5, hình thang có hai đáy song song và hai cạnh đáy bằng nhau là hình bình hành.
- Đúng vì khi đó ta được tứ giác có hai cặp cạnh đối song song chính là hình bình hành (định nghĩa)
Xem thêm:
Dấu hiệu nhận biết tiếp tuyến của đường tròn