Việc được sử dụng máy tính để tính những phương trình, hàm số hay tổ hợp chỉnh hợp đã là đều hết sức bình thường đối với học sinh trung học. Bên cạnh đó cũng sẽ có những bạn hoàn toàn chưa rõ về cách bấm máy tính tiệm cận. Vậy nên hãy cùng Reviewedu.net tìm hiểu qua bài viết sau để có thể cải thiện khả năng của mình nhé!
Tiệm cận trong toán học là gì?
Trong giải tích toán học, tiệm cận là một thuật ngữ mô tả các hành vi tại vô cùng,gồm tiệm cận ngang,tiệm cận đứng.
Ví dụ, giả sử ta quan tâm đến thuộc tính của hàm f(n) khi n rất lớn. Nếu f(n) = n2 + 3n, thì khi n rất lớn, số hạng 3n trở nên không đáng kể so với n2. Hàm f(n) được gọi là “tương đương tiệm cận với n2, khi n → ∞ “. Kí hiệu f(n) ~ n2, cũng đọc là ” f(n) tiệm cận đến n2 “.
Các công thức của tiệm cận
Để tìm đường tiệm cận của hàm số y = f(x) ta dựa vào tập xác định D để biết số giới hạn phải tìm. Nếu tập xác định D có đầu mút là khoảng thì phải tìm giới hạn của hàm số khi x tiến đến đầu mút đó.
Ví dụ: D = [a ; b) thì phải tính ![]() thì ta phải tìm ba giới hạn là
thì ta phải tìm ba giới hạn là
– Để tìm đường tiệm cận ngang ta phải có giới hạn của hàm số ở vô tận:
![]() thì (Δ) : y = y0 là tiệm cận ngang của (C) : y = f(x).
thì (Δ) : y = y0 là tiệm cận ngang của (C) : y = f(x).
– Để tìm đường tiệm cận đứng thì hàm số phải ra vô tận khi x tiến đến một giá trị x0 :
Nếu ![]() thì (Δ) : x = x0 là đường tiệm cận đứng của (C) : y = f(x).
thì (Δ) : x = x0 là đường tiệm cận đứng của (C) : y = f(x).
– Để tìm đường tiệm cận xiên của (C) : y = f(x), trước hết ta phải có điều kiện
![]() Sau đó để tìm phương trình đường tiệm cận xiên ta có hai cách :
Sau đó để tìm phương trình đường tiệm cận xiên ta có hai cách :
+ Phân tích biểu thức y = f(x) thành dạng y = f(x) = ax + b + ε(x) ![]() thì (Δ) : y = ax + b
thì (Δ) : y = ax + b
(a ≠ 0) là đường tiệm cận xiên của (C) : y = f(x) ![]()
+ Hoặc ta tìm a và b bởi công thức:
Khi đó y = ax + b là phương trình đường tiệm cận xiên của (C) : y = f(x).
Cách bấm máy tính tiệm cận
Để tìm tiệm cận của đồ thị hàm số ta làm theo 3 bước sau
- Bước 1: Nhập biểu thức hàm số vào máy tính
- Bước 2: Bấm CACL các đáp án
- Bước 3: Tính giới hạn
Cách 1: Sử dụng bản lĩnh SOLVE nhằm giải nghiệm. Nếu mẫu số là hàm bậc ( 2 ) hoặc bậc ( 3 ) thì ta hoàn toàn có thể dùng tuấn kiệt Equation ( EQN) nhằm tìm nghiệm Bước 2: Dùng nhân tài CALC để test phần đông nghiệm tìm được bao gồm là nghiệm của tử số hay là không.Cách 3: Những quý hiếm ( x_0 ) là nghiệm của chủng loại số nhưng lại ko là nghiệm của tử số thì mặt đường thẳng ( x=x_0 ) là tiệm cận đứng của hàm số.
Bài tập áp dụng cách bấm máy tính tiệm cận
Ví dụ 1: Trích đề minh họa lần 2 của bộ giáo dục và đào tạo
Tìm tất cả các tiệm cận đứng của đồ thị hàm số y=2x−1−x2+x+3√x2−5x+6
- x = – 3 và x = -2
- x = – 3
- X = 3 và x = 2
- x = 3
Phân tích
Mẹo: Tiệm cận đứng x = a thì tại giá trj đó thường làm cho mẫu không xác định và
limx→ay=∞
Do đó ta CALC các đáp án xem có đáp án nào báo Error không
Lời giải
Bước 1: Nhập hàm số vào màn hình máy tính
Kết luận: Đồ thị hàm số này có 3 đường tiệm cận
Nếu đề bài hỏi rõ là tìm tiệm cận đứng hoặc tiệm cận ngang của đồ thị hàm số thì bạn làm theo hướng dẫn sau đây
Xem thêm:



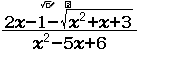



có khó không anh chị?
tiệm cận học lớp 12 hả anh chị?
hướng dẫn em cách bấm với :((((