Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức nesbit. Vậy bất đẳng thức nesbit là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức nesbit là gì?
Trong toán học, b là một trường hợp đặc biệt của bất đẳng thức Shapiro khi số phần tử là 3. Nó được phát biểu như sau:
Cho a,b,c là ba số thực dương. Khi đó ta có:
Chứng minh bất đẳng thức nesbit
Chứng minh
Bất đẳng thức này có nhiều cách chứng minh. Dưới đây trình bày 2 cách.
Cách thứ nhất
Bắt đầu từ bất đẳng thức Nesbitt (đề xuất năm 1903)
Biến đổi vế trái:
Thêm một bước biến đổi:
Chia cả hai vế cho 3 và chuyển vế:
Vế trái là trung bình cộng, vế phải là trung bình điều hoà, do vậy bất đẳng thức đúng, ta có điều cần chứng minh.
(Ta cũng có thể sử dụng trung bình nhân của ba biến để chứng minh).
Cách thứ hai
Không mất tổng quát, giả sử a>=b>=c, ta có:
Đặt:
Tích vô hướng của 2 vectơ trên cực đại theo Bất đẳng thức hoán vị nếu chúng được xếp cùng hướng. Đặt và là các vector thu được từ chuyển tương ứng 1 và 2 vị trí, ta có:
Cộng 2 bất đẳng thức trên ta được bất đẳng thức Nesbitt.
Cách thứ ba
đặt S= a/(b+c) + b/(c+a) + c/(a+b)
M= b/(b+c) + c/(c+a) + a/(a+b)
N= c/(b+c) + a/(c+a) + b/(a+b)
có M+N=3
áp dụng bất đẳng thức AM-GM
M+S>=3
N+S>=3
=>M+N+2S>=6
=>2S+3>=6
=>S>=3/2(đpcm)
Bài tập ứng dụng bất đẳng thức nesbit
Bài tập 1. Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng: 1 a2 (b + c) + 1 b2 (c + a) + 1 c2 (a + b) ≥ 3 2
Lời giải. Ta có: ∑ 1 a2 (b + c) = ∑ abc a2 (b+ c) = ∑ bc ab + ca ≥ 3 2 Đẳng thức xảy ra khi và chỉ khi a = b = c = 1
Bài tập 2. Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng: a (b + c) 2 + b (c + a) 2 + c (a + b) 2 ≥ 9 4 (a + b + c)
Lời giải. Ta viết lại bất đẳng thức: (a + b+ c) ( a (b + c)2 + b (c + a)2 + c (a + b)2 ) ≥ 9 4 Theo bất đẳng thức Cauchy − Schwarz có: (a + b + c) ( a (b + c)2 + b (c + a)2 + c (a + b)2 ) ≥ ( a b+ c + b c + a + c a + b )2 ≥ 9 4 Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
Bài tập 3. Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng: 1 a (b + 1) + 1 b (c + 1) + 1 c (a + 1) ≥ 3 2
Lời giải. Đặt a = x/y, b = y/z, c = z/x, ta có: ∑ 1 a (b + 1) = ∑ yz xy + zx ≥ 3 2 Đẳng thức xảy ra khi và chỉ khi a = b = c = 1.
Bài tập 4. Cho a, b > 0 và x, y, z là các số dương tuỳ ý. Tìm giá trị nhỏ nhất của: x2 (ay + bz)(az + by) + y2 (az + bx)(ax+ bz) + z2 (ax+ by)(ay + bx)
Lời giải. Theo bất đẳng thức AM −GM có: (ay + bz)(az + by) ≤ (ay + bz + az + by) 2 4 = (a + b)2(y + z)2 4 ≤ (a + b) 2(y2 + z2) 2 Suy ra, x2 (ay + bz)(az + by) ≥ 2x 2 (a + b)2(y2 + z2) Tương tự, ta có: y2 (az + bx)(ax+ bz) ≥ 2y 2 (a + b)2(z2 + x2) z2 (ax + by)(ay + bx) ≥ 2z 2 (a + b)2(x2 + y2) Do đó, ∑ x2 (ay + bz)(az + by) ≥ 2 (a + b)2 ( x2 y2 + z2 + y2 z2 + x2 + z2 x2 + y2 ) ≥ 3 (a + b)2
Xem thêm:



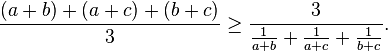


có mấy cách để giải bất đẳng thức này ạ?
Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng: a (b + c) 2 + b (c + a) 2 + c (a + b) 2 ≥ 9 4 (a + b + c). Cứu em bài này ạ
bất đẳng thức này là gì vậy ạ?