Hình thang là một cái tên quen thuộc trong lĩnh vực toán học. Chắc hẳn hình thang đã trở thành người bạn, thường xuyên xuất hiện và mang đến hơi thở mới mẻ trong những bài toán hình học. Để tìm hiểu rõ hơn và có cái nhìn toàn cảnh về hình thang, dưới đây là những kiến thức lý thuyết về hình thang mà Review Edu đem đến cho các bạn: Hình thang là gì, tính chất, dấu hiệu nhận biết, cách tính diện tích hình thang và chu vi hình thang.
Hình thang là gì?
Trong hình học Euclide đã định nghĩa hình thang là một tứ giác lồi có hai cạnh đối song song. Hai cạnh song song này được gọi là hai cạnh đáy, hai cạnh còn lại gọi là hai cạnh bên của hình thang.
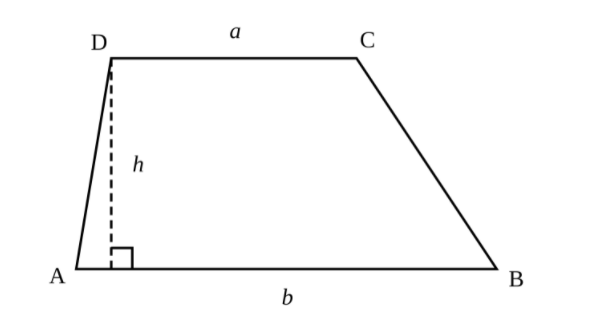
Trong đó:
h là chiều cao hình thang
a: Độ dài đáy bé
b: Độ dài đáy lớn
Dấu hiệu nhận biết hình thang
Để dễ dàng nhận biết hình thang, bạn có thể dựa vào 5 dấu hiệu nhận biết dưới đây:
- Tứ giác có hai cạnh đối song song
- Hình thang có một góc vuông được gọi hình thang vuông
- Hình thang có hai góc kề một đáy thì gọi là hình thang cân
- Hình thang có hai cạnh bên bằng nhau được gọi là hình thang cân
- Hình thang có hai đường chéo bằng nhau được gọi là hình thang cân
Các tính chất của hình thang
Tính chất về góc:
Tổng của hai góc kề một cạnh bên của hình thang bằng 180°( hai góc đó nằm ở vị trí trong cùng phía của hai đoạn thẳng song song – 2 cạnh đáy)
Tính chất về cạnh:
– Một hình thang mà có hai cạnh đáy bằng nhau thì hai cạnh bên của hình thang đó sẽ song song và bằng nhau.
– Ngược lại một hình thang có hai cạnh bên song song thì hai cạnh đó sẽ bằng nhau và hai cạnh đáy của chúng sẽ bằng nhau.
Chu vi hình thang
Chu vi hình thang bằng tổng độ dài tất cả các cạnh của hình thang.
Trong đó:
P là ký hiệu chu vi
a,b,c,d là các cạnh của hình thang
Ví dụ: Tính chu vi của hình thang, biết đáy lớn bằng 12cm; đáy bé bằng 10 cm; hai cạnh bên lần lượt bằng 6cm và 7cm
Lời giải: Gọi hình thang cần tính chu vi là ABCD. Từ công thức tính chu vi hình thang, ta có:
Chu vi hình thang ABCD là P (ABCD) = 12 + 10 + 6 + 7= 35 cm
Diện tích hình thang
Có 2 cách tính diện tích hình thang, đó là:
– Diện tích hình thang bằng tích của tổng hai cạnh đáy với chiều cao chia hai.
– Diện tích hình thang bằng trung bình cộng hai cạnh đáy nhân với chiều cao.
Bài thơ sau giúp công thức tính diện tích hình thang trở nên dễ nhớ hơn:
Muốn tính diện tích hình thang
Đáy lớn đáy nhỏ ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
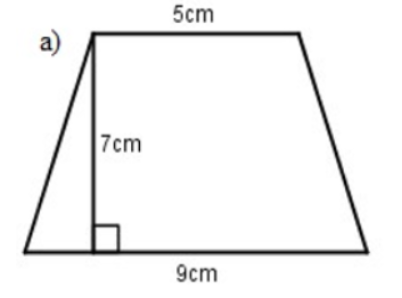
Ví dụ: Hãy tính diện tích hình thang sau biết độ dài đáy là 5cm và 9cm, chiều cao là 7cm.
Từ công thức tính diện tích hình thang, ta có:
S = [(5 + 9) x 7] : 2= 49 cm2 hoặc S = [(5+9) : 2] x 7 = cm2
Vậy diện tích của hình thang trên là 49cm2
Chiều cao hình thang
Công thức tính chiều cao hình thang bằng diện tích hình thang nhân 2, chia cho tổng chiều dài 2 đáy.
Ví dụ: Một hình thang có diện tích bằng 40m2 và độ dài các cạnh đáy lần lượt bằng 4m, 6m. Từ đó tính chiều cao của hình thang đó.
Vận dụng công thức tính chiều cao hình thang, ta có:
h = (S x 2) : ( a +b) = ( 40 x 2) : ( 4+6) = 8 (m)
Vậy độ dài chiều cao hình thang đã cho là 8m.
Đường trung bình của hình thang
Đường trung bình của hình thang là gì?
Đường trung bình của hình thang được định nghĩa theo cách đơn giản đó chính là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.
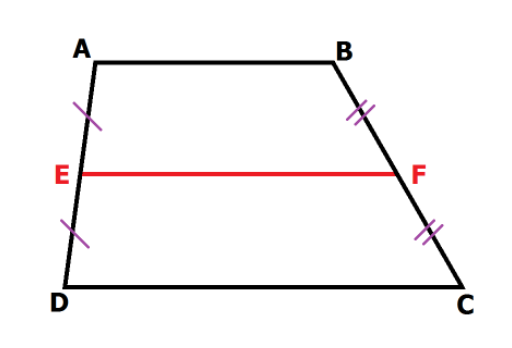
Cách tính đường trung bình của hình thang
Đường trung bình của hình thang bằng tổng độ dài hai đáy chia hai
Ví dụ: Cho hình thang ABCD có AB bằng 5 cm và CD bằng 7 cm , trong đó I và K lần lượt là trung điểm của AD và BC. Chứng minh IK là đường trung bình của hình thang ABCD và tính độ dài của EF.
Hình thang ABCD có I là trung điểm của AD, K là trung điểm của BC nên IK là đường trung bình của hình thang ABCD.
Áp dụng công thức đường trung bình của hình thang, ta có:
IK = ( AB + CD) : 2 = ( 5+7) : 2 = 6 cm.
Vậy IK là đường trung bình của hình thang ABCD và có độ dài bằng 6cm
Định lý Talet trong hình thang
Nếu một đường thẳng song song với hai đáy và cắt hai cạnh bên của hình thang thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
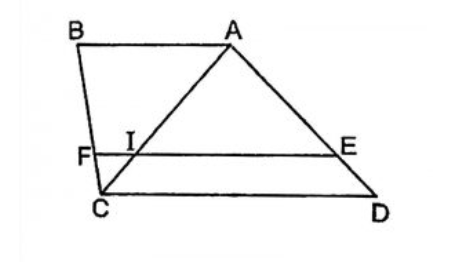
Cho hình thang ABCD, biết rằng điểm E thuộc cạnh AD và F thuộc cạnh BC
Nếu EF // AB // CD, ta có AE/DE = BF/CF
Ngược lại, nếu: AE/DE = BF/CF → EF // AB// CD
Ví dụ: Cho hình thang ABCD ( AB // CD) biết rằng AB là đáy bé, CD là đáy lớn. Đường thẳng MN song song với hai đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2 cm, AM = 3 cm, BC = 6 cm. Tính độ dài BN.
Theo đề bài, hình thang ABCD có AB // CD // MN
Dựa vào định lý Talet trong hình thang ABCD ta có,
AMAD = BN BC BN = AM.BCAD= 3.62= 9 cm
Vậy nên độ dài đoạn BN là 9 cm.
Bài tập áp dụng về hình thang
Bài tập 1: Cho hình thang ABCD (AB//CD) có ∠A = 60°, ∠C = 100°. Tính số đo các góc còn lại của hình thang?
Lời giải
Hình thang ABCD có AB//CD nên ta có:
*) ∠A + ∠D = 180°
⇔ 60° + ∠D = 180°
⇔ ∠D = 180° – 60° = 120°.
Vậy ta có ∠D = 120°.
*) ∠B + ∠C = 180°
⇔ ∠B + 100° = 180°
⇔ ∠B = 180° – 100° = 80°.
Vậy ta có ∠B = 80°.
Bài tập 2: Cho hình thang ABCD có AB // CD có AB = 3cm, CD = 5cm, khoảng cách giữa hai đường thẳng AB và CD bằng 3cm. Tính diện tích hình thang ABCD.
Lời giải:
Diện tích hình thang ABCD là
3 x((3 + 5)/2) = 12 (cm2)
Đáp số: 12 cm2
Bài tập 3: Cho hình thang ABCD với AB = AD = 3cm, CD = 5cm, BC = 4cm. Tính chu vi hình thang ABCD?
Lời giải:
Chu vi hình thang ABCD là:
P = AB + BC + CD + AD = 3 + 4 + 5 + 3 = 15(cm)
Cùng nhau tổng hợp kiến thức về hình thang và ôn tập nhé !



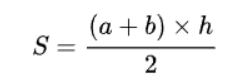
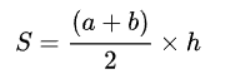
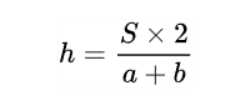
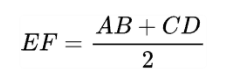


đường trung bình của hình thang là gì?
như thế nào gọi là hình thang
có những dấu hiệu nhận biết hình thang nào?