Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức số phức. Vậy bất đẳng thức số phức là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Số phức là gì?
Trong tiếng Anh số phức có nghĩa là Complex Number. Từ complex cũng có nghĩa là phức hợp. Có nghĩa sô’ phức bao gồm nhiều thành phần để cấu tạo nên nó. Cụ thể tập số phức gồm các số có dạng a+bi. Trong đó a và b là các số thực và i là đơn vị ảo thỏa mãn i² = -1.
Mô đun của số phức
Với mỗi sô’ phức z=a+bi (a, b∈R) thì mô đun của sô’ phức z là một số thực ký hiệu là |z| (đọc là mô đun của z). Và được tính theo công thức:
Số phức liên hợp
Với mỗi sô’ phức z=a+bi (a, b∈R) thì sô’ phức liên hợp của z là
Biểu diễn hình học của số phức
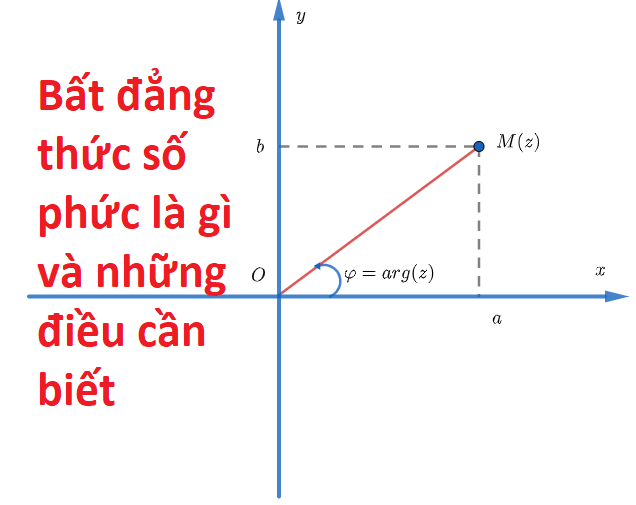
Mỗi số phức z=a+bi (a, b∈R) được đặt tương ứng với điểm M(z)=(a;b) trên mặt phẳng tọa độ Oxy. Tương ứng này là 1 song ánh. Do đó các bài toán về hình học và các bài toán về số phức có thể chuyển hóa qua lại cho nhau.
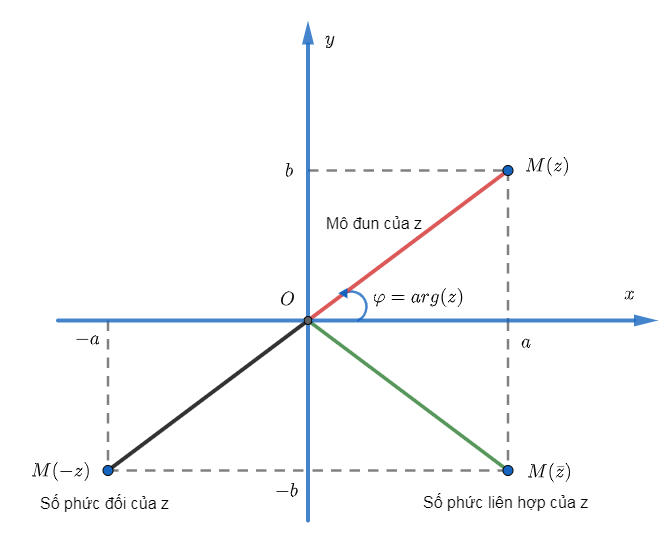
Các khái niệm tương ứng cũng được thể hiện trên hình sau:
Hình chiếu của M(z) lên trục Ox là phần thực của z. Do đó trục Ox còn gọi là trục thực. Các số thực đều được biểu diễn bởi nằm trên trục Ox. Hình chiếu của M(z) lên trục Oy là phần ảo của z. Do đó trục Oy còn gọi là trục ảo. Các số thuần ảo đều được biểu diễn bởi điểm nằm trên trục Oy. Số z và số phức liên hợp của z được biểu diễn bởi 2 điểm đối xứng nhau qua trục thực. Mô đun của z chính là khoảng cách giữa điểm M(z) và gốc tọa độ.
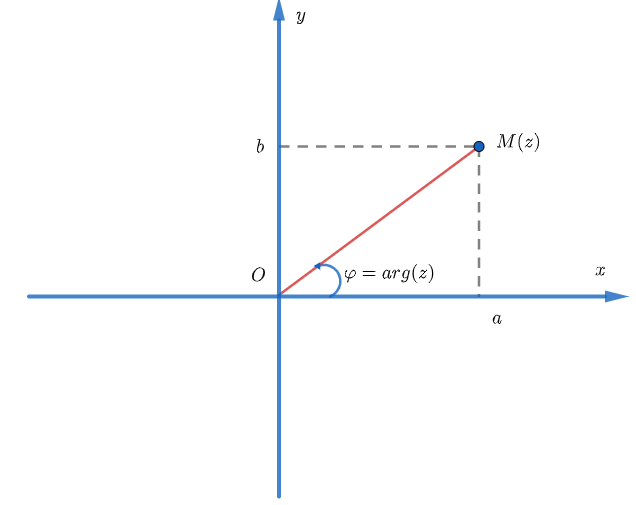
ARGUMENT CỦA SỐ PΗỨC
Giả sử M(z) là điểm biểu diễn cho z. Khi đó góc giữa tia Ox và tia OM(z) được gọi là argument của z.
Bài tập ứng dụng bất đẳng thức số phức
A.8 B. 10 C. 8 D.√10
Hướng dẫn giải:
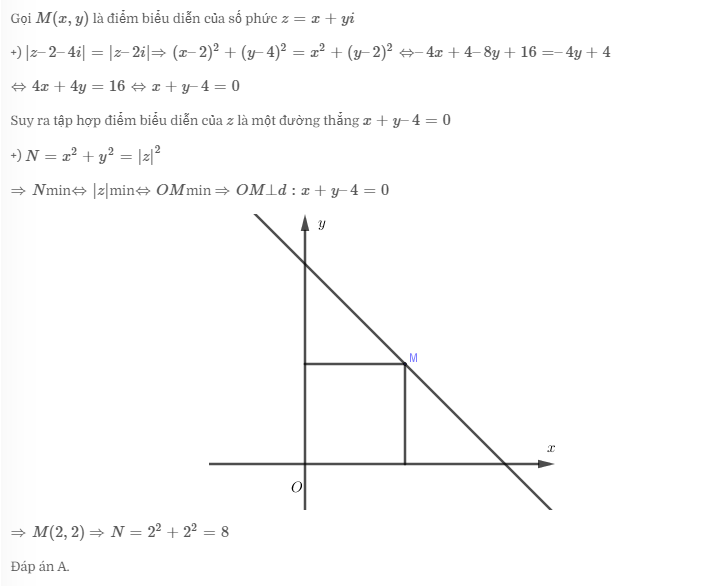
Bài tập 2: Vẽ tập hợp điểm biểu diễn của số phức. Từ đó tìm max, min của mô đun
A.8 B.10 C.16 D.26


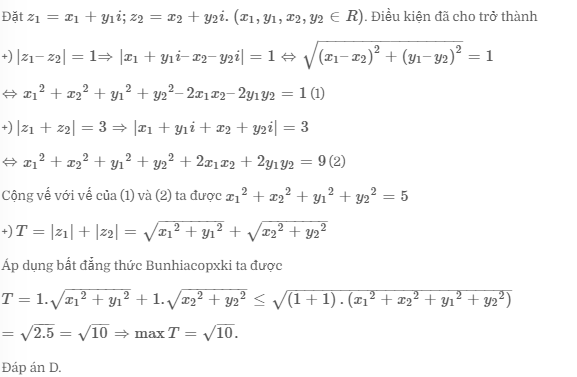
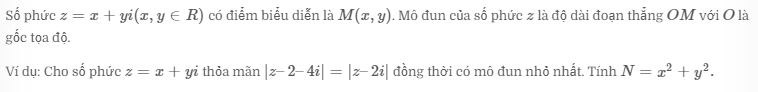


bất đẳng thức này là gì?
có khó không ạ?
có cần phải chứng minh bất đẳng thức không?