Bất đẳng thức đáng nhớ là kiến thức quan trọng trong chương trình Toán học cho các em học sinh. Có rất nhiều bất đẳng thức mà học sinh phải ghi nhớ khi còn ngồi trên ghế nhà trường. Một trong số đó là bất đẳng thức Vecto. Vậy bất đẳng thức mincopxki là gì, công thức vận hành như thế nào thì hãy cùng Reviewedu.net tìm hiểu qua bài viết dưới đây nhé!
Bất đẳng thức Vectơ Là gì?
Trong toán học sơ cấp, vecto (Vector trong tiếng Anh hay trong Hán-Việt là hướng lượng) là một đoạn thẳng có hướng. Ví dụ trong mặt phẳng cho hai điểm phân biệt A và B bất kì ta có thể xác định được vecto AB.
Trong toán học cao cấp, một vecto là một phần tử trong một không gian vectơ, được xác định bởi ba yếu tố: điểm đầu (hay điểm gốc), hướng (gồm phương và chiều) và độ lớn (hay độ dài).
Chứng minh bất đẳng thức vecto
Ví dụ 1: Cho bốn số thực tùy ý ![]() . Chứng minh:
. Chứng minh:
Lời giải:
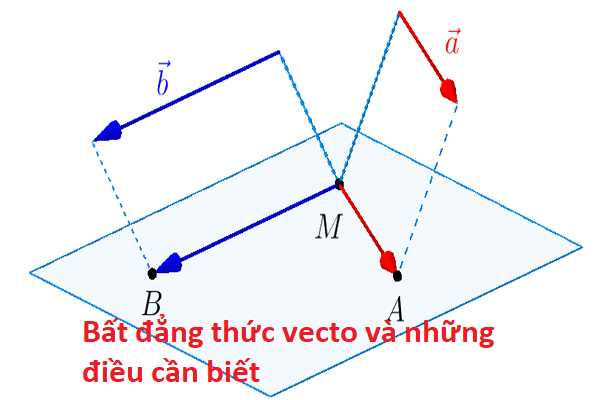
Ví dụ 2: Cho 4 điểm A, B, C, D Chứng minh rằng:
Lời giải:
Cách 1: Biến đổi vế trái (VT) ta có:
Nhận xét: Sử dụng cách giải này, ta cần chú ý khi biến đổi các số hạng của một vế cần quan tâm phân tích làm xuất hiện các số hạng có ở vế bên kia. Chẳng hạn số hạng ở vế trái là ![]() nhưng vế phải có chứa
nhưng vế phải có chứa ![]()
Bài tập ứng dụng bất đẳng thức vecto
Ví dụ 1: Cho ΔABC, CMR: cosA + cosB + cosC ≤3/2
Lời giải:
Thiết lập các vectơ đơn vị ![]() trên các cạnh AB, BC, AC của ΔABC, ta được:
trên các cạnh AB, BC, AC của ΔABC, ta được:
Ví dụ 2: Cho ΔABC, CMR: cos2A + cos2B + cos2C ≥ -3/2
Lời giải:
Gọi O là tâm đường tròn ngoại tiếp ΔABC, ta nhận được:
Xem thêm:
Bất đẳng thức mincopxki là gì và những điều cần biết




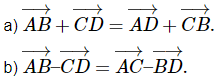
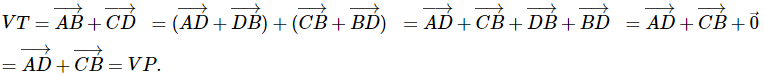
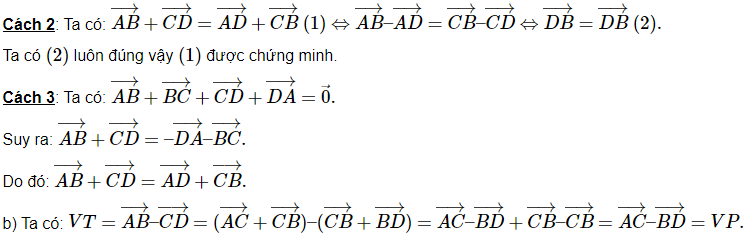
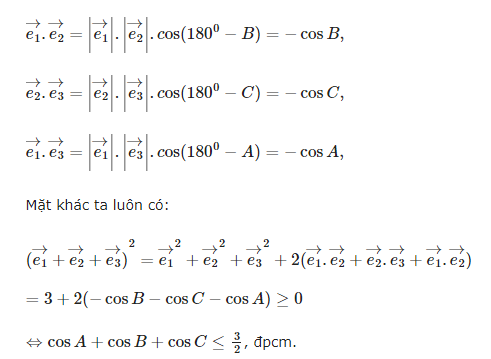
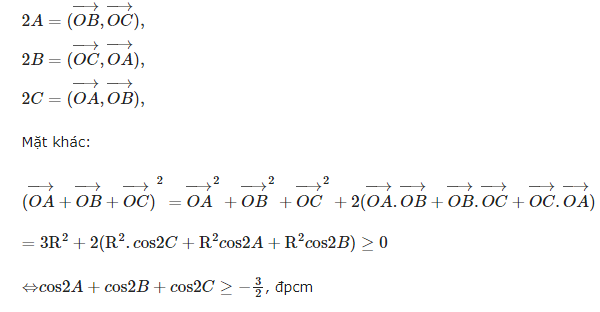


bất đẳng thức vector khó không?
có cần phải chứng minh bất đẳng thức này không?
là bất đẳng thức gì vậy ạ?